Battle Engine

Battle Engine Explained

Definitions

Match	A complete fight between two characters. A match has n rounds.
Round	A round includes two turns, one for the attacker and one for defender
Turn	A turn includes n hits with n between 1 and 3
Armor Encumbrance	Ratio between the Equipped Armor weight and the base transportable weight
Armor Penetration	Armor penetration represents a weapon's ability to overcome armor to deliver cutting damage.

How it works

Initiative Computation

Initiative determine who will attack first and is computed at the start of every round. It will depend on the reach attribute of each character’s weapon. A character using a weapon with a longer reach than his/her opponent will have better odds of gaining the initiative. If the weapons have the same reach, each character has a equal chance of gaining the initiative.

  Initiative = f( Attacker_Weapon_Length, Defender_Weapon_Length )

Consecutive Hits Computation

Range: 1-3

After initiative has been computed, the engine computer how many consecutive hits the attacker will deal.

Negative Variables

• Weapon Reach
• Weapon Weight
• Armor Encumbrance

Positive Variables

• Energy
• Constitution
• Strength

The variables values will be normalized and summed.

	strength + energy + constitution (normalized) (normalized)
weapon reach + weapon weight + armor encumberance (normalized)		0	0,5	1	1,5	2	2,5	3
	0	1	1	2	3	3	3	3
	0,5	1	1	2	3	3	3	3
	1	1	1	1	2	3	3	3
	1,5	1	1	1	1	2	3	3
	2	1	1	1	1	2	3	3
	2,5	1	1	1	1	1	2	3
	3	1	1	1	1	1	2	3

Hit and Miss Chance Computation

Logic to hit or miss depends on the ratio between Attacker and Defender Dexterities.

  Hit_chance = f( Attacker_Dexterity, Defender_Dexterity )

If a character is stunned the attacker has a 100% chance to hit the opponent.

Example:

• Attacker has dex 20, defender has dex 15. Hit_Chance will be about 71%.
• Attacker has dex 20, defender has dex 2. Hit_Chance will be about 97%.
• Attacker has dex 10, defender has dex 18. Hit_Chance will be about 55%.
• Attacker has dex 1, defender has dex 18. Hit_Chance will be about 26%.

Hit Logic

It will be possible to hit on following body parts:

head, armor, legs, feet, left arm, right arm

Only with a weapon of reach at least 4, it will be possible to hit the part feet.

The armors will do not (as before) covers only the part where they are equipped but they extend also on other parts.

For example, before the plate armor was equipped on slot armor and its defense was effective only when the attacker was hitting the part “armor”. Now, the plate armor defense is effective also against hits on left arm and right arm.

Armor	Equipped on	Covers
Chainmail	Torso	Armor, Left Arm, Right Arm
Leather Armor	Armor	Armor
Plate Armor	Armor	Armor, Left Arm, Right Arm

Example

If the defender is wearing a chainmail (defense 4) under a Leather Armor (defense 2), and a hit goes on part Armor:

1. The engine will recompute damage by applying the Leather Armor + chainmail defense (6)
2. The engine will consume only the Leather Armor but by his defense (2)

If the Leather Armor eventually breaks the engine will consider only the Chainmail Defense and then consume the Chainmail. If the hit is landed on the left arm and the defender holds a shield, the damage will be absorbed by all the Shield.

Damage Computation

Dealt damage depends from the following factors:

• Weapon Damage
• Weapon Condition
• Strength
• Energy
• Defender AC

Base Damage

The Base Damage is randomly selected within the range of damage values for the equipped weapon. With a Strength value of 10, an energy value of 50%, and a weapon condition of 50%, the damage will be randomly selected using a Normal (Gaussian) distribution centered on the mean of the weapon’s damage range. Thus, if the range is 1-7, a 4 will have the best odds of being rolled and a 1 and a 7 would have the worst odds of being rolled.

• With increasing Strength, Energy and Weapon Condition, the distribution is skewed more toward the maximum of the range.
• With decreasing Strength, Energy and Weapon Condition, the distribution is skewed more toward the minimum of the range.

  Base Damage = max(1, Weapon Damage + (Weapon Damage * Character Strength / 23) )

Example

Attacker hits with a longsword, Computed Weapon Damage is 6. Attacker has strength 18.

  Base Damage = 6 + 6 * (18/23) = 10.7

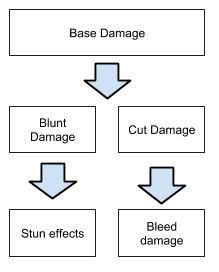
The Base Damage is then partitioned in Blunt Damage and Cutting Damage accordingly to the weapon Cutting Damage/Blunt Damage.

Example

  Base Damage of longsword = 10.7. Longsword has Blunt 20% and Cut 80%. Blunt Damage = 2.14 and Cut Damage = 8.56

Blunt Damage and Armor Consumption

Blunt damage is the damage inflicted by the inertia of a weapon impacting an opponent and it depends from the choosen weapon. Weapons with high blunt damage are meant to destroy and consume opponent armor.

In addition, blunt damage brings a chance to stun an opponent, which causes the character to:be unable to attack or defend. The chance of stunning an opponent is proportional to the amount of blunt damage inflicted.

Damage and armor consumption are as follow:

If bluntdamage is >= than equipment defense:

  if (hit part is shield)
     bluntdamage = bluntdamage - equipment_defense * 0.4
     cutdamage = 0
  else
     bluntdamage = bluntdamage - equipment_defense
     cutdamege = ... 
  consumption = max(1, equipment_defense)/wearfactor

If bluntdamage is < than equipment defense:

  bluntdamage = 0
  consumption = bluntdamage

Wearfactor is always 1 except Special Sets.

Example 1

Attacker hits with a longsword for a damage 10 and hits the shield with defense 2

BEFORE DEFENSE

Bluntdamage = 8.56, Cut Damage = 2.14, Total Damage = 10.7

AFTER DEFENSE

Damage = 8, Shield wears off by 6.56% (bluntdamage - shield defense)

Example 2

Attacker hits with a longsword for a damage 10.7 and hits the shield with defense 10

BEFORE DEFENSE

Bluntdamage = 8.57, Cut Damage = 2.16, Total Damage = 10.7

AFTER DEFENSE

Bluntdamage = 8.48, Cut Damage = 2.16, Total Damage =

Damage = 0, Shield wears off by 10%

Stun Effects

If a character is stunned, he can be stunned for n turns, where the number of turns for which the opponent is stunned depends on opponent constitution:

  Rounds_stunned = f (constitution);

When the player is stunned:

1. The player is unable to attack the opponent and to defend himself;
2. All of the opponent’s attack swings are successfully dealt;
3. Basic damage incurred from the opponent is increased by 150%

Cutting Damage

Cutting damage is the damage inflicted by the weapon slicing into flesh of an opponent. Cutting damage causes the initial damage but also bleed damage, which is inflicted each turn until the battle is terminated.

  Cuttingdamage After Defense = cuttingdamage / ( 1 - (equipmentdefense * 3.5)/Armor penetration)

  Bleed Damage = cuttingdamage * 0.05

Example:

Attacker uses a longsword. Base Damage = 10,7. Cutting Damage = 8.57

Mario hits Paolo for 8.57 cutting damage. This will result in about 1.714 HP Bleed Damage. ... Mario hits Paolo for 8.57 cutting damage. This will result in about 1.714+1.714 = 3.42 HP Bleed Damage.

Weapon Consumption

Weapon is consumed accordingly to the following formula:

If the hit part had an equipment with defense:

  Weapon Consumption = max(1, equipment_defense * 0,5)/wearfactor * 0.25

else

  Weapon Consumption = 1/wearfactor * 0.25

Example 1

Attacker hits with a longsword for a damage 10 and hits the shield with defense 10

BEFORE DEFENSE

Bluntdamage = 8, Cut Damage = 2, Total Damage = 10

AFTER DEFENSE Damage = 0, Longsword wears off by 1.25%

Example 2

Attacker hits with a longsword for a damage 10 and hits the head (no armor)

BEFORE DEFENSE

Bluntdamage = 8, Cut Damage = 2, Total Damage = 10

AFTER DEFENSE

Damage = 10, Longsword wears off by 0.25%

Wear Factor

Weapons and Armor is consumed while fighting. Every Weapon and Armor has a Wear Factor that is used to correct the weapon consumption.

  Weapon/Armor Consumption = Consumption * Wear Factor

For example, if a weapon after a succesfull hit it should ne consumed by 0.01 and has a wear factor of 0.5, it will consumed by 0.005.

The Critical Hit

A Critical Hit can deal severe damage. Only some Weapons can deliver a Critical Hit. Please check [Weapons] page to find out. The chance of delivering a critical hit will depend from the weapon that the player is using and from the difference between attacker and defender intelligence and dexterity.

If a weapon has a Critical factor of 19x2 it means that to deliver a Critical Hit with that weapon one must score at least 19 on a d20. Once established that a weapon scores a Critical, opponentes Intelligence and Dexterity are evaluated.

Intel + Dex Diff	Percentage to score a Critical	War Hammer Critical Chance: 5%	Long Sword Critical Chance: 10%	Scimitar Critical Chance: 15%	The Punisher Critical Chance;20%
		Combined Percentage
0		1%	1%	2%	2%
1	1,00%	1%	1%	2%	2%
2	1,28%	1%	1%	2%	2%
3	1,41%	1%	1%	2%	3%
4	1,51%	1%	2%	2%	3%
5	1,58%	1%	2%	3%	3%
6	1,64%	1%	2%	3%	4%
7	1,70%	1%	2%	3%	4%
8	1,74%	1%	2%	3%	4%
9	1,79%	1%	2%	4%	5%
10	1,83%	1%	3%	4%	5%
11	1,86%	1%	3%	4%	5%
12	1,89%	1%	3%	4%	6%
13	1,92%	2%	3%	5%	6%
14	1,95%	2%	3%	5%	7%
15	1,98%	2%	4%	5%	7%
16	2,00%	2%	4%	6%	7%
17	2,03%	2%	4%	6%	8%
18	2,05%	2%	4%	6%	8%
19	2,07%	2%	4%	6%	9%
20	2,09%	2%	5%	7%	9%
21	2,11%	2%	5%	7%	9%
22	2,13%	2%	5%	7%	10%
23	2,15%	3%	5%	8%	10%
24	2,17%	3%	5%	8%	11%
25	2,19%	3%	6%	8%	11%
26	2,20%	3%	6%	9%	12%
27	2,22%	3%	6%	9%	12%
28	2,23%	3%	6%	9%	13%
29	2,25%	3%	6%	10%	13%
30	2,26%	3%	7%	10%	13%
31	2,28%	3%	7%	10%	14%
32	2,29%	4%	7%	11%	14%
33	2,31%	4%	7%	11%	15%
34	2,32%	4%	8%	11%	15%
35	2,33%	4%	8%	12%	16%
36	2,34%	4%	8%	12%	16%
37	2,36%	4%	8%	13%	17%
38	2,37%	4%	9%	13%	17%
39	2,38%	4%	9%	13%	18%
40	2,39%	5%	9%	14%	18%
41	2,40%	5%	9%	14%	19%
42	2,42%	5%	10%	14%	19%
43	2,43%	5%	10%	15%	20%
44	2,44%	5%	10%	15%	20%

Energy consumption

Energy is very important in battle (for example you see in the previous formula that impacts the number of consecutive hits). The Energy depletion formula will depends on the following variables

Negative variables

• Weapon Reach
• Weapon Weight
• Armor Encumbrance

Positive variables

• Constitution

The above variables values will been normalized as per the following theory: How to Normalize Data so thwy will be converted to values between 0 to 1.

	weapon reach + weapon weight + armor encumbrance (normalized)
constitution (Normalized)		0	0,5	1	1,5	2	2,5	3
	0	1,33	1,50	1,67	1,83	2,00	2,17	2,33
	0,5	1,17	1,33	1,50	1,67	1,83	2,00	2,17
	1	1,00	1,17	1,33	1,50	1,67	1,83	2,00
	1,5	0,83	1,00	1,17	1,33	1,50	1,67	1,83
	2	0,67	0,83	1,00	1,17	1,33	1,50	1,67
	2,5	0,50	0,67	0,83	1,00	1,17	1,33	1,50
	3	0,33	0,50	0,67	0,83	1,00	1,17	1,33

Armor Encumbrance

Armor Encumbrance is computed as follows:

  Armor Encumbrance = (Equipped items weight (weapon excluded)/Base_Transportable_Weight

where

  Base_transportable_weight =  100 - power(abs(  strength  - 23 ), 1.3) Kg