Difference between revisions of "Battle Engine"
(→Energy consumption) |
|||
| Line 136: | Line 136: | ||
Energy is very important in battle (for example you see in the previous formula that impacts the number of consecutive hits). | Energy is very important in battle (for example you see in the previous formula that impacts the number of consecutive hits). | ||
| − | The | + | The Energy depletion formula will depends on the following variables |
| − | * Weapon | + | '''Negative variables''' |
| − | * | + | * Weapon Reach |
| − | + | * Weapon Weight | |
| − | * | + | * Armor Encumbrance |
| − | + | '''Positive variables''' | |
| − | + | * Constitution | |
| + | |||
| + | where Armor Encumbrance is | ||
| + | |||
| + | <pre>sum of weight (equipped clothes, armor except weapon)/transportable weight</pre> | ||
| + | |||
| + | The above variables values will been normalized as per the following theory: [http://stats.stackexchange.com/questions/70801/how-to-normalize-data-to-0-1-range] so thwy will be converted to values from 0 to 1. | ||
| + | |||
| + | {|class='wikitable' | ||
| + | ! | ||
| + | !colspan="8"|weapon reach + weapon weight + armor encumbrance (normalized) | ||
| + | |- | ||
| + | !rowspan="9"|constitution (Normalized) | ||
| + | | | ||
| + | |0 | ||
| + | |0,5 | ||
| + | |1 | ||
| + | |1,5 | ||
| + | |2 | ||
| + | |2,5 | ||
| + | |3 | ||
| + | |- | ||
| + | |0 | ||
| + | |1,33 | ||
| + | |1,50 | ||
| + | |1,67 | ||
| + | |1,83 | ||
| + | |2,00 | ||
| + | |2,17 | ||
| + | |2,33 | ||
| + | |- | ||
| + | |0,5 | ||
| + | |1,17 | ||
| + | |1,33 | ||
| + | |1,50 | ||
| + | |1,67 | ||
| + | |1,83 | ||
| + | |2,00 | ||
| + | |2,17 | ||
| + | |- | ||
| + | |1 | ||
| + | |1,00 | ||
| + | |1,17 | ||
| + | |1,33 | ||
| + | |1,50 | ||
| + | |1,67 | ||
| + | |1,83 | ||
| + | |2,00 | ||
| + | |- | ||
| + | |1,5 | ||
| + | |0,83 | ||
| + | |1,00 | ||
| + | |1,17 | ||
| + | |1,33 | ||
| + | |1,50 | ||
| + | |1,67 | ||
| + | |1,83 | ||
| + | |- | ||
| + | |2 | ||
| + | |0,67 | ||
| + | |0,83 | ||
| + | |1,00 | ||
| + | |1,17 | ||
| + | |1,33 | ||
| + | |1,50 | ||
| + | |1,67 | ||
| + | |- | ||
| + | |2,5 | ||
| + | |0,50 | ||
| + | |0,67 | ||
| + | |0,83 | ||
| + | |1,00 | ||
| + | |1,17 | ||
| + | |1,33 | ||
| + | |1,50 | ||
| + | |- | ||
| + | |3 | ||
| + | |0,33 | ||
| + | |0,50 | ||
| + | |0,67 | ||
| + | |0,83 | ||
| + | |1,00 | ||
| + | |1,17 | ||
| + | |1,33 | ||
| + | |} | ||
==War Encumbrance== | ==War Encumbrance== | ||
Revision as of 13:25, 26 January 2016
Contents |
Battle Engine Explained
Definitions
| Match | A complete fight between two characters. A match has n rounds. |
| Round | A round includes two turns, one for the attacker and one for defender |
| Turn | A turn includes n hits with n between 1 and 3 |
| War encumbrance | encumbrance in battle is the ratio between the equipped item weight and the base transportable weight |
| Armor Penetration | Armor penetration represents a weapon's ability to overcome armor to deliver cutting damage. The values reflect what percentage of a weapon’s cutting damage is inflicted on the opponent wearing armor with rating of AC 1. Thicker armor deflects more of the cutting damage. |
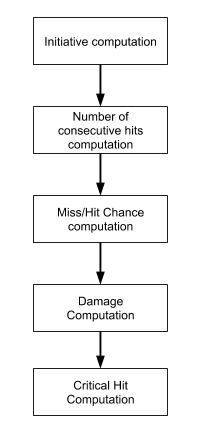
How it works
Initiative Computation
Initiative determine who will attack first and is computed at the start of every round. It will depend on the reach attribute of each character’s weapon. A character using a weapon with a longer reach than his/her opponent will have better odds of gaining the initiative. If the weapons have the same reach, each character has a equal chance of gaining the initiative.
Initiative = f( Attacker_Weapon_Length, Defender_Weapon_Length )
Consecutive Hits Computation
Range: 1-3
After initiative has been computed, the engine computer how many consecutive hits the attacker will deal. Consecutive hits are negatively affected by the attacking character’s weapon weight and weapon length, and positively affected by the attacking character’s strength and energy levels.
Stunned characters cannot attack.
Consecutive attacks number = f( Attacker_Weapon_Length, Strength, Energy )
Hit and Miss Chance Computation
Logic to hit or miss depends on the ratio between Attacker and Defender Dexterities.
Hit_chance = f( Attacker_Dexterity, Defender_Dexterity )
If a character is stunned the attacker has a 100% chance to hit the opponent.
Example:
- Attacker has dex 20, defender has dex 15. Hit_Chance will be about 71%.
- Attacker has dex 20, defender has dex 2. Hit_Chance will be about 97%.
- Attacker has dex 10, defender has dex 18. Hit_Chance will be about 55%.
- Attacker has dex 1, defender has dex 18. Hit_Chance will be about 26%.
Damage Computation
Dealt damage depends from the following factors:
- Weapon Damage
- Weapon Condition
- Strength
- Energy
- Defender AC
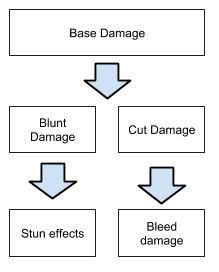
Base Damage
Base Damage = f ( Weapon_Damage, Weapon_Condition, Strength, Energy) + Strength / 6
The Base Damage is randomly selected within the range of damage values for the equipped weapon. With a Strength value of 10, an energy value of 50%, and a weapon condition of 50%, the damage will be randomly selected using a Normal (Gaussian) distribution centered on the mean of the weapon’s damage range. Thus, if the range is 1-7, a 4 will have the best odds of being rolled and a 1 and a 7 would have the worst odds of being rolled.
- With increasing Strength, Energy and Weapon Condition, the distribution is skewed more toward the maximum of the range.
- With decreasing Strength, Energy and Weapon Condition, the distribution is skewed more toward the minimum of the range.
The Base Damage is then partitioned in Blunt Damage and Cutting Damage accordingly to the weapon Cutting Damage/Blunt Damage. For example if the Base Damage with a Fauchard is 10, Blunt damage will be 5 and Cutting Damage 5. Check Weapons Table for useful data.
Blunt Damage
Blunt damage is the damage inflicted by the inertia of a weapon impacting an opponent. It depends from the choosen weapon. Blunt damage brings a chance to stun an opponent, which causes the character to:be unable to attack or defend. The chance of stunning an opponent is proportional to the amount of blunt damage inflicted.
Stun_Change = f( blunt_damage )
Example:
Attacker uses Fauchard. Base Damage = 10. Blunt Damage = 5. The defender is on the head, where the helmet has defense = 1. The final Blunt Damage will be 4 and the stun chance will be 2.67%.
Effects of stun
If a character is stunned, he can be stunned for n turns, where the number of turns for which the opponent is stunned depends on opponent constitution:
Rounds_stunned = f (constitution);
When the player is stunned:
- The player is unable to attack the opponent and to defend himself;
- All of the opponent’s attack swings are successfully dealt;
- Basic damage incurred from the opponent is increased by 150%
Cutting Damage
Cutting damage is the damage inflicted by the weapon slicing into flesh of an opponent. Cutting damage causes the initial damage but also bleed damage, which is inflicted each turn until the fight is concluded.
Effects of bleed damage:
Bleed damage is the damage caused by blood loss coming from a cutting wound. It is a percentage of the cumulative cutting damaged incurred. Every successful hit will accumulate a certain amount bleed damage that depends from the weapon penetration.
Example:
Attacker uses Fauchard. Base Damage = 10. Cutting Damage = 5.
Mario hits Paolo for 5 cutting damage. This will result in about 0.125 HP Bleed Damage. Paolo receives another hits and his Bleed Damage accumulates to 0.3 HP. At each turn Paolo will receive an additional damage of 0.3 HP.
The Critical Hit
Once established that a character hits the opponent, a check is done for a critical hit. The chance to deal a critical hit depends on:
- Used weapon
- Attacker intelligence vs Defender intelligence
Critical chance = f (IntelligenceAttacker, Intelligencedefender)
A critical hit multiplies the damage for a factor related to the used weapon.
Example
Guglielmo uses a Fauchard and deal a basic damage 8. Fauchard has a Critical Factor 20-4. This means that a 20-faces dices must score 20 in order to deal a Critical Hits. If 20 is scored the basic damage is multiplied by 4, and becomes 32. The Basic Damage is then splitted to 16 blunt damage and 16 cut damage.
Energy consumption
Energy is very important in battle (for example you see in the previous formula that impacts the number of consecutive hits). The Energy depletion formula will depends on the following variables
Negative variables
- Weapon Reach
- Weapon Weight
- Armor Encumbrance
Positive variables
- Constitution
where Armor Encumbrance is
sum of weight (equipped clothes, armor except weapon)/transportable weight
The above variables values will been normalized as per the following theory: [1] so thwy will be converted to values from 0 to 1.
| weapon reach + weapon weight + armor encumbrance (normalized) | ||||||||
|---|---|---|---|---|---|---|---|---|
| constitution (Normalized) | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | |
| 0 | 1,33 | 1,50 | 1,67 | 1,83 | 2,00 | 2,17 | 2,33 | |
| 0,5 | 1,17 | 1,33 | 1,50 | 1,67 | 1,83 | 2,00 | 2,17 | |
| 1 | 1,00 | 1,17 | 1,33 | 1,50 | 1,67 | 1,83 | 2,00 | |
| 1,5 | 0,83 | 1,00 | 1,17 | 1,33 | 1,50 | 1,67 | 1,83 | |
| 2 | 0,67 | 0,83 | 1,00 | 1,17 | 1,33 | 1,50 | 1,67 | |
| 2,5 | 0,50 | 0,67 | 0,83 | 1,00 | 1,17 | 1,33 | 1,50 | |
| 3 | 0,33 | 0,50 | 0,67 | 0,83 | 1,00 | 1,17 | 1,33 | |
War Encumbrance
War encumbrance is computed as follows:
War encumbrance = (Equipped items weight)/Base_Transportable_Weight
where
Base_transportable_weight = 100 - power(abs( strength - 20 ), 1.3) Kg